Simulacro · Examen 1

a) (1 punto) Las energías potencial gravitatoria y cinética que tiene el satélite en su órbita. b) (1 punto) La energía que fue necesario comunicar al satélite para ponerlo en órbita desde la superficie de la Tierra. \textbf{Datos:} Constante de Gravitación Universal, \( G = 6{,}67 \cdot 10^{-11} \, \text{Nm}^2\text{kg}^{-2} \) ; Masa de la Tierra, \( M_T = 5{,}97 \cdot 10^{24} \, \text{kg} \) ; Radio de la Tierra: \( R_T = 6{,}37 \cdot 10^3 \, \text{km} \)

\( \textbf{Ejercicio 2.} \quad (\text{Calificación máxima: 2 puntos}) \) A lo largo de una cuerda se propaga en el sentido \( +x \) una onda transversal. El periodo de oscilación y la elongación máxima de un punto cualquiera de la cuerda son, respectivamente, \( 4 \cdot 10^{-3} \, \text{s} \) y \( 3 \, \text{mm} \). La distancia mínima entre dos puntos cualesquiera de la cuerda que oscilan en fase es de \( 0{,}25 \, \text{m} \). En el instante \( 2 \cdot 10^{-3} \, \text{s} \) la elongación de un punto situado a \( 0{,}5 \, \text{m} \) del origen de coordenadas es de \( -1{,}5 \, \text{mm} \) y su velocidad de oscilación en ese instante es positiva. a) (1 punto) Halle la frecuencia angular y la velocidad de propagación de la onda. b) (1 punto) Obtenga la expresión matemática que describe la onda.

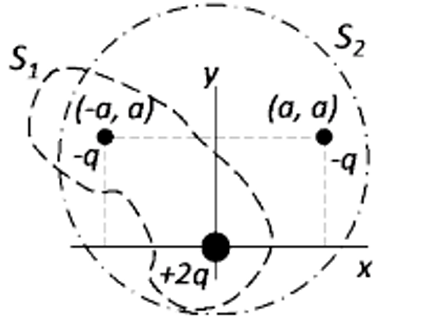
\( \textbf{Ejercicio 3.} \quad (\text{Calificación máxima: 2 puntos}) \) Tres cargas \( -q \), \( -q \) y \( +2q \) se encuentran situadas en los puntos del plano \( (-a,a) \), \( (a,a) \) y \( (0,0) \) respectivamente, tal y como se describe en la figura. Determine, en función de la constante de Coulomb \( K \), el valor de la carga \( q \), y la distancia \( a \): a) (1 punto) La expresión de la fuerza electrostática que se ejerce sobre la carga situada en \( (a,a) \), y la expresión del trabajo que habrá realizado esa fuerza electrostática para traer la carga \( -q \) desde el infinito hasta la posición \( (a,a) \). b) (1 punto) El flujo del campo eléctrico a través de las superficies cerradas \( S_1 \) y \( S_2 \). \( \textbf{Datos:} \) Permeabilidad eléctrica del vacío \( \varepsilon_0 = \frac{1}{4 \pi K} \)

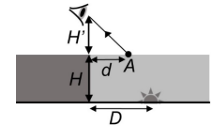
\( \textbf{Ejercicio 4.} \quad (\text{Calificación máxima: 2 puntos}) \) Un observador está situado al borde de un estanque de profundidad \( H = 2 \, \text{m} \). Su visual está a una altura \( H' = 1{,}6 \, \text{m} \) sobre la superficie del agua. En el fondo del estanque hay un foco puntual de luz. El observador lo ve cuando mira hacia el punto \( A \) de la superficie a una distancia \( d = 1{,}2 \, \text{m} \) del borde (véase la figura). Calcule: a) (1 punto) El índice de refracción del agua del estanque si la longitud de onda de la luz del foco vale \( 375 \, \text{nm} \) en ella y \( 500 \, \text{nm} \) en el aire. b) (1 punto) La distancia \( D \) del foco a la pared del estanque. Datos: Velocidad de la luz en el vacío, \( c = 3 \cdot 10^8 \, \text{m} \cdot \text{s}^{-1} \); Índice de refracción del aire, \( n = 1 \).

\( \textbf{Ejercicio 5.} \quad (\text{Calificación máxima: 2 puntos}) \) En un laboratorio de preparación de radiofármacos se rompe accidentalmente una botella de una solución que contenía \( ^{18}\text{F} \) con una actividad de 18,5 MBq. a) (1 punto) Calcule la masa de \( ^{18}\text{F} \) derramada. b) (1 punto) Determine el tiempo que ha de transcurrir hasta que la actividad se reduzca a 37 kBq. \(\textit{Datos:}\) \(\tau = 109{,}7 \, \text{minutos} \quad \text{(Vida media del } ^{18}\text{F})\) \(M_F = 18 \, \text{g mol}^{-1} \quad \text{(Masa molar del } ^{18}\text{F})\) \(N_A = 6{,}02 \cdot 10^{23} \, \text{mol}^{-1} \quad \text{(Número de Avogadro)}\)